Ισχύει ο κανόνας του Leonardo για τα δένδρα;
Διάβασα κάπου για τον "κανόνα του Leonardo για τα δέντρα" και όχι απλά εντυπωσιάστηκα αλλά έμεινα έκθαμβος! Τι κατάφερε να δει το πιο παρατηρητικό -ίσως- μάτι ανθρώπου που έζησε ποτέ; Αλλά και πώς μπορεί ένα απλό αλλά εμφανέστατο φαινόμενο να μην έχει γίνει τόσο ευρέως γνωστό (να το μαθαίνουμε ας πούμε στο Δημοτικό), ως ο βασικός κανόνας της ανάπτυξης των δέντρων;
Ο Da Vinci θεώρησε ότι βρήκε τον κανόνα με βάση τον οποίο διακλαδώνονται ο κορμός και κατόπιν τα κλαδιά των δέντρων. Ο κανόνας στηρίζεται σε μια αρχή διατήρησης, η οποία για τον Da Vinci ήταν η επιφάνεια διατομής. Δηλαδή, το άθροισμα της επιφάνειας διατομής των θυγατρικών κλάδων αμέσως μετά τη διακλάδωση, είναι ίσο με τη επιφάνεια του κλάδου/κορμού γονέα. Αν λοιπόν ένα δέντρο ανοίγεται ως βεντάλια, τότε μαζεύοντας πάλι τη βεντάλια παίρνουμε έναν "σωλήνα" με ύψος όσο και αυτό του δέντρου. Ακούγεται απλό, οικονομικό (ως αρχή διατήρησης) και επίσης συμμετρικό. Γιατί να μην είναι αλήθεια;
Ο κανόνας θεωρούνταν μέχρι πρόσφατα "μάλλον" αληθής, καθώς ελλείψει ακριβών μετρήσεων δεν είχε πάρει τη μορφή αναγκαστικής νομοτέλειας. Για τους ημιμαθείς ήταν άλλη μια φαεινή ιδέα του Leonardo, δείγμα τού πώς η αξεπέραστη παρατηρητικότητά του, συνδυασμένη με την ενόραση της μεγαλοφυίας, ερμήνευε για αλλη μια φορά ορθά τον κόσμo. Είναι όμως σωστός ο κανόνας ή μήπως πρόκειται για λάθος της διαίσθησης;
Τα τελευταία χρόνια εμφανίστηκαν κάποιες επιστημονικές μελέτες και προσπάθειες σοβαρής μαθηματικοποίησης του θέματος. Θα σας δείξω τι βρήκα καθώς έψαξα στο διαδίκτυο και επίσης πού κατέληξα μετά τη μελέτη αυτών των διαφορετικών προσεγγίσεων.
Ξεκινάμε με τη μελέτη/μοντέλο (Πηγή 1) του φυσικού Christophe Eloy, καθηγητή στο Πανεπιστήμιo της Προβηγκίας, ο οποίος ειδικεύεται στην αεροδυναμική. Τα αποτελέσματα της μελέτης του έγιναν αποδεκτά για δημοσίευση το 2011 από το πολύ έγκυρο Physical Review Letters.
Ο Elloy δημιούργησε ένα διδιάστατο μαθηματικό μοντέλο ανάπtυξης δένδρου με βάση τα fractals. Δηλαδή πήρε μια μορφή αρχικής διακλάδωσης και την επέβαλλε σε κάθε διαδοχική διακλάδωση, παίρνοντας έτσι στο τέλος έναν θύσανο. Όταν υπέβαλλε το μοντέλο σε προσομοίωση αεροδυναμικής σήραγγας, παρατήρησε την ιδιαίτερη αντοχή τού δέντρου σε διάφορες ταχύτητες ανέμου, αν ίσχυε ο κανόνας του Leonardo για το πάχος των διαδοχικών κλάδων.
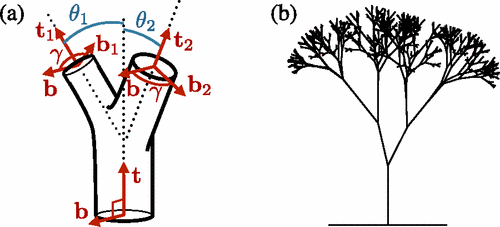
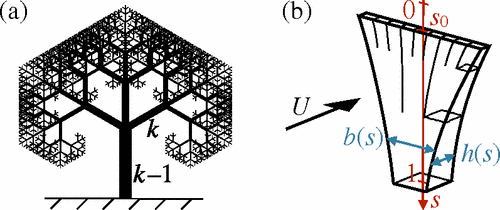
Με βάση αυτή την προσομοίωση κατέληξε ότι όχι μόνο ισχύει ο κανόνας αλλά και γίνεται "επί σκοπόν", δηλαδή υπάρχει αεροδυναμικός λόγος για τον οποίο προκύπτει η μορφή των δέντρων: μεγαλώνουν με τον "κανόνα" κατά νου. Η δημοσίευση έκανε μεγάλη εντύπωση, η οποία συνεχίζεται μέχρι σήμερα. Μάλιστα λόγω της κομψότητας της ερμηνείας αλλά και του θρύλου της αυθεντίας του Leonardo, που πάντοτε δονεί την δημοσιότητα, η "αεροδυναμική επιβεβαίωση" του κανόνα αναπαράγεται κατά κόρον στο διαδίκτυο (βλ. Πηγές 2, 3).
Εγώ όμως έχω ενδοιασμούς. Πρώτα από όλα, είναι διδιάστατη και όχι τρισδιάστατη η ερμηνεία, ενώ ο Leonardo τις τρεις διαστάσεις είχε στο νου του, άσχετα αν είχε δίκιο ή όχι. Πρόκειται λοιπόν για μια επίπεδη προβολή του κανόνα. Δεν νομίζω επίσης πως έχει νόημα να μιλήσουμε για αεροδυναμικό "στόχο" σε αειθαλή δέντρα (όπως π.χ. το έλατο ή η ελιά). Εκεί το φύλλωμα παίζει αποφασιστικό(τερο) ρόλο στο αεροδυναμικό σχήμα του δέντρου. Αυτό από μόνο του καταρρίπτει την καθολικότητα του αεροδυναμικού σκοπού.
Επιπλέον, η ίδια η έννοια ενός "σκοπού" είναι προβληματική. Πώς γνωρίζει το φυτό κατά τη στιγμή της διακλάδωσης πόσο ακριβώς μελλοντικό πάχος θα αποκτήσει; Το "ξέρει" βεβαίως στο fractal μοντέλο, καθώς είναι έτσι προγραμματισμένο. Αλλά δεν μπορεί ένα φυσικό κλαδί να είναι το ίδιο "προγραμματισμένο", καθώς μεγαλώνει, ώστε να αποκτήσει το ακριβές πάχος που απαιτείται για την τήρηση του αεροδυναμικού στόχου. Αν στην πρώτη π.χ. διακλάδωση έχει κάπου, κάπως, αποθηκευτεί αυτή η απλή πληροφορία για το πάχος του κλάδου γονέα, σε ύστερες γενεές διακλαδώσεων δεν μπορεί ένα κλαδί να γνωρίζει τον αριθμό και τα μεγέθη των κλάδων της γενέας του (με τα οποία συναθροίζει το πάχος του) και επίσης τα αντίστοιχα μεγέθη της προηγούμενης "πατρικής" γενεάς.
Ψάχνοντας περισσότερο βρήκα και άλλες μελέτες, πιο πρόσφατες αυτές, όπως των Ρώσων S.V. Grigoriev, O.D. Smyrnov, P.M. Pustovoy, E.G. Lashina και K.A. Pshenichnyi που δημοσιεύτηκε στο επίσης εγκυρότατο Physical Review το 2022. Αυτοί πήραν φωτογραφίες από πραγματικά δέντρα (οξυά και βαλανιδιά), δηλαδή πραγματικές διδιάστατες παραστάσεις δέντρων. Αυτό που βρήκαν, αφού ανέλυσαν μαθηματικώς την κατανομή παχών με τη μεθοδο Fourier, βρήκαν ότι αυτό που διατηρείται στο διδιάστατο επίπεδο είναι το γινόμενο πάχους d (η προβολή της διαμέτρου στο επίπεδο της φωτογραφία) με το ύψος του κλαδιού l. Δηλαδή αν κάποιο κλαδί (i-γενιά) διακλαδωθεί σε k κλαδιά ίσου πάχους και ύψους (i+1 γενιά) τότε ισχύει (𝑑𝑖) x (𝑙𝑖)=𝑘 x (𝑑𝑖+1) x (𝑙𝑖+1).
Στην πράξη, αυτό που λένε είναι ότι διατηρείται όχι η διατομή (όπως έλεγε ο Leonardo και παρέπεμπε σε διατήρηση όγκου), αλλά η επιφάνεια του στέλεχους (η κατακόρυφη προβολή, ως πάχος επί ύψος) σε κάθε γενεά. Χωρίς να προτείνουν κάποια "στόχευση", αυτό που προκύπτει από την έρευνα και τη μέτρηση είναι η διατήρηση καθ' ύψος της διδιάστατης επιφάνεια αντίστασης στον άνεμο. Αυτό (μια ψηλή στήλη σταθερού πάχους), από μόνο του δεν είναι το βέλτιστο αεροδυναμικό σχήμα: όσο πιο ψηλό είναι το δέντρο τόσο ψηλώνει το σημείο που εφαρμόζεται η συνισταμένη δύναμη του αέρα (πρέπει να τοποθετείται λίγο πιο πάνω από το μέσο του, καθώς ο αέρας αυξάνει σε ταχύτητα με το ύψος). Άρα αξάνεται και η ροπή που τείνει να ξεριζώσει το δέντρο. Συνεπώς, η όλη κατασκευή θα πρέπει να στηρίζεται από ικανό ριζικό σύστημα ώστε να διατηρηθεί το δέντρο όρθιο.
Τελειώνοντας με αυτή την "δομική" προσέγγιση, απορώ πώς και γιατί σταματά σε κάποιο μέγεθος η ανάπτυξη του δέντρου; Στην περίπτωση της fractal κατασκευής του Eloy, το όριο ανάπτυξης είναι εκ των προτέρων προγραμματισμένο. Αλλά δεν μπορούμε να δεχτούμε ανάλογο προγραμματισμό στη φυσική περίπτωση. Αν λοιπόν έχουμε (σε κάποια είδη δέντρων) έναν κανόνα τήρησης επιφάνειας που σχηματοποιείται ως υψωμένη στήλη, τότε πότε σταματά να ψηλώνει η στήλη; Πρέπει να υπάρχει (και) κάποιος άλλος μηχανισμός που να ελέγχει την ανάπτυξη του δέντρου.
Αυτός ο άλλος μηχανισμός είναι υδροδυναμικής φύσης και αφορά την κυκλοφορία του νερού από το ριζικό σύστημα μέχρι τα άκρα του φυλλώματος. Γνωρίζουμε για τα τριχοειδή φαινόμενα, δηλαδή την περίεργη συμπεριφορά του νερού όταν περνά μέσα από "σωλήνες" πολύ μικρής διατομής, όπως οι φλέβες μας αλλά και τα αγγεία που μεταφέρουν το θρεπτικό υδατοδιάλυμα από τις ρίζες στα φύλλα των φυτών και των δέντρων. Mέσα σε αυτά τα μικρά αγγεία το νερό αψηφά τη βαρύτητα, παίρνει την ανηφόρα και μάλιστα με τόσο περισότερη δύναμη όσο μικρότερη είναι η διατομή του αγγείου. Πολύ ωραίες ασκήσεις σχετικά με το φαινόμενο των τριχοειδών αγγείων βρίσκονται στην Πηγή 5. Επίσης, παραθέτω στην Πηγή 9 και μια ωραία εξήγηση του μοριακού επιπέδου του φαινομένου της διαβροχής (ανύψωσης του νερού) των τοιχομάτων του σωλήνα.
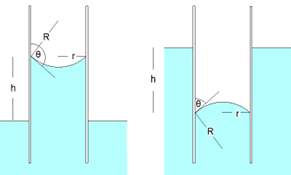
Ο λόγος που συμβάνουν τα τριχοειδή φαινόμενα είναι ότι όσο μικρότερη η διατομή του σωλήνα (τριχοειδής) τόσο πιο έντονη είναι η αλληλεπίδραση της μοριακής δομής του νερού (είναι διπολικής μορφής, με τα υδρογόνα προς τη μια άκρη και το οξυγόνο προς την άλλη) και των αντίστοιχων μορίων των τοιχωμάτων. Ανάλογα με το είδος των μορίων των τοιχωμάτων μπορεί να έχουμε είτε άνοδο είτε κάθοδο του ύψους του νερού, αλλά και συγκεκριμένη γωνία μεταξύ επιφάνειας του νερού και του τοιχώματος (βλέπε το διπλανό σχήμα). Στην περίπτωση των φυτών έχουμε καμπύλωση προς τα πάνω και άνοδο.
Μάλιστα το ύψος της διαβροχής είναι αντιστρόφως ανάλογο της διαμέτρου h∝1/R. Ή διαφορετικά, h*R=σταθ. Αν λοιπόν μειώσουμε τη διατομή κατά το μισό και βάλουμε τους δύο σωλήνες δίπλα-δίπλα, θα έχουμε διπλάσιο ύψος διαβροχής. Στην πρόσοψη (στη διδιάστατη όρθια όψη) θα έχουμε το νερό να ανεβαίνει σε μια στήλη ίσου πάχους (κάθε φορά που οι διατομές θα υποδιπλασιάζονται θα ανεβαίνει κατά h). Από την πλευρά του όρθιου παρατηρητή θα είχαμε διατήρηση του πάχους και -φαινομενικά- του όγκου της στήλης. Χονδρικά, αυτή είναι και η εντύπωση του δένδρου θα που αποκόμιζε ο Da Vinci και κάθε άλλος όρθιος παρατηρητής. Από πάνω όμως, ο παρατηρητής που βλέπει κάθετα τη διατομή, δε βλέπει διατήρηση της επιφάνειας άρα και του όγκου. Δείτε πώς φαίνεται από πάνω η πολύ μικρότερη συνολική επιφάνεια των δύο κίτρινων διατομών (κάθε μία με μισή ακτίνα από την αρχική), σε σχέση με την επιφάνεια του αρχικού σωλήνα (μπλε).
Και μόνο από αυτή την εποπτική εικόνα καταλαβαίνουμε ότι η διαίσθηση του Leonardo μάλλον λανθάνει για το σύνολο του δέντρου, μια και δεν διατηρείται η επιφάνεια (και αντίστοιχα ο όγκος) καθώς αναπτύσσεται το δέντρο. Αλλά, όπως είπαμε και προηγουμένως, και μόνο τα έλατα και τις ελιές να δεις κανείς από το έδαφος, ως όρθιος παρατηρητής, καταλαβαίνει ότι ο "κανόνας" δεν μπορεί να είναι καθολικός.
Παρατηρώντας προσεκτικά το ίδιο το σχέδιο του Leonardo βλέπουμε πώς οι σχεδιαστικές του προσομειώσεις τον οδηγούν στο λάθος συμπέρασμα. Στην αριστερή πλευρά του σχεδίου το στέλεχος διαιρείται στα δύο, για την ακρίβεια σε δύο κλάδους ίσου πάχους και μήκους. Στη δεξιά πλευρά του σχεδίου, αναπτύσσει το δένδρο κατά "δακτυλίους" που ισαπέχουν (κατά αυξανόμενη ακτίνα). Στον πρώτο δακτύλιο έχουμε δύο στελέχη, στον δεύτερο τέσσερα, στον τρίο οκτώ. Μέχρις εδώ και διατηρώντας το μήκος καθώς υποδιπλασιάζει το πάχος-ακτίνα του νέου κλαδιού, έχουμε διατήρηση της διδιάστατης επιφάνειας και μπορούμε να μιλάμε για δομικού χαρακτήρα διαμόρφωση (με τις όποιες αεροδυναμικές επιπτώσεις).
Από τον τέταρτο όμως δακτύλιο και μετά τα πράγματα μπερδεύονται ακόμα και για έναν Leonardo. Τέρμα οι υποδιπλασιαμοί και η διατήρηση μήκους.
Όπως δείχνει στο κάτω δεξιά σχήμα, ο Da Vinci θεωρούσε/παρατηρούσε δέντρα "θύσανους" (και φυσικά φυλλοβόλα). Με την αίσθηση συμμετρίας, η οποία πίστευε ότι επικρατεί παντού στη φύση, προέβαλλε την ιδέα της συμμετρίας και στην ανάπτυξη των δέντρων (μια αρχή διατήρησης) και διατύπωσε τον περίφημο "κανόνα των δέντρων".
Φαίνεται όμως ότι μετά από αιώνες ήρθε η ώρα να προσεγγιστεί επιστημονικά το θέμα (τόσο μαθηματικά/θεωρητικά όσο και πειραματικά). Πέρα από τις πιο πάνω μελέτες/έρευνες των Eloy (ο οποίος στην πράξη μόνο ένα δικό του θεωρητικό μοντέλο έχει κάνει) αλλά και των Ρώσων, οι οποίοι έχουν πολύ καλά αντιληφθεί την διδιάστατη πλευρά του φιανομένου στηριζόμενοι σε πραγματικές μετρήσεις (φωτογραφίες), το 2023 δημοσιεύτηκε στο Proceedings of the National Academy of Science (Πηγή 6) η μελέτη των Ruben Valbuena (Bangor University) και Stuart Sopp (Swedish University of Agricultural Sciences), η οποία φαίνεται να δίνει την ορθή εικόνα του φαινομένου και να το ερμηνεύει με μια πιο στέρεα αρχή διατήρησης, αυτή της υδροδυναμικής αντίστασης, η οποία παραπέμπει στην πιο καθολική οικονομική αρχή της φύσης, αυτή της ελάχιστης δράσης.
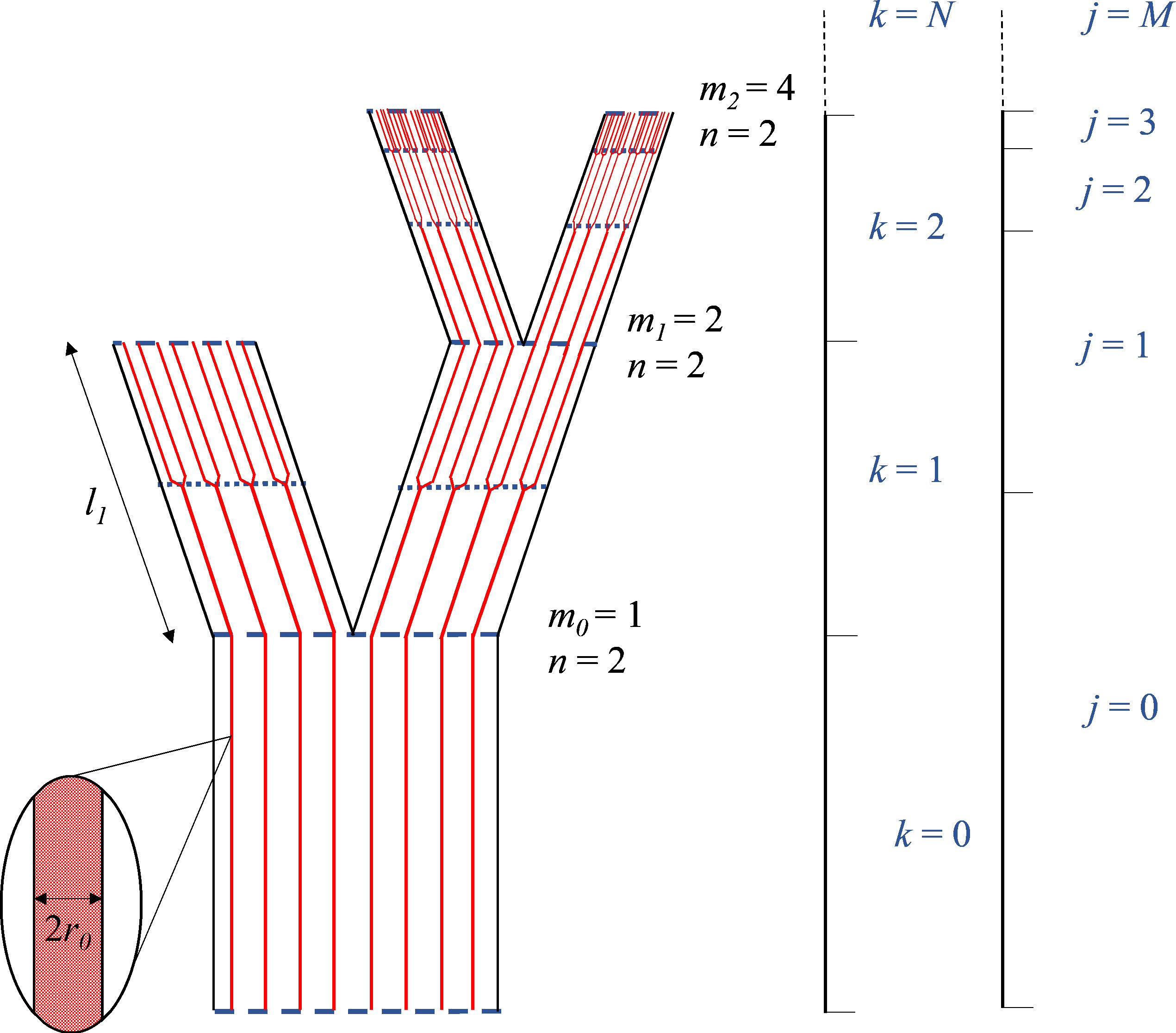
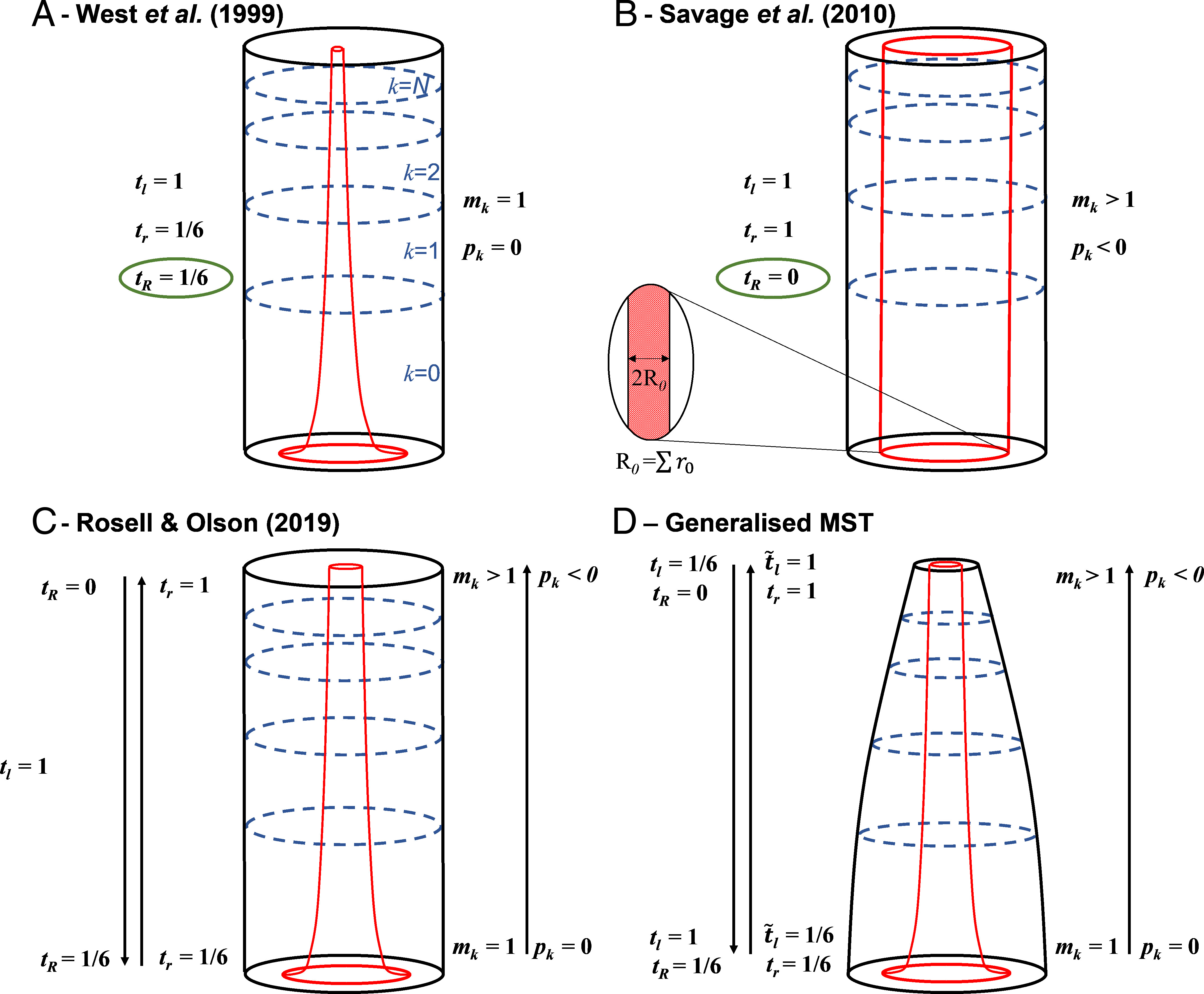
Όπως φαίνεται στο πάνω αριστερά σχήμα, τα σωληνοειδή αγγεία ακολουθούν τις βασικές διακλαδώσεις (κορμοί/κλαδιά), αλλά διακλαδίζονται και τα ίδια πριν την επόμενη βασική διακλάδωση, μειώνοντας αντίστοιχα τις διατομές τους. Όσο ανεβαίνουμε σε βασικές διακλαδώσεις τόσο πιο γρήγορα διακλαδίζονται τα αγγεία. Τα αγγεία συνενώνονται σταδιακά (coalescence) και συνιστούν τον εξωτερικό φλοιό του κλάδου.
Υπάρχει σοβαρός λόγος γι΄αυτό το φινόμενο και είναι εμφανέστερος στα ψηλά δέντρα. Τα αγγεία έχουν δύο ξεχωριστές λειτουργικές περιοχές: αυτή που ξεκινά από τον κορμό και φτάνει μέχρι λίγο πριν το φύλλωμα και κατόπιν η επόμενη περιοχή, από εκεί όπου ξεκινούν και μέχρις εκεί που καταλήγουν οι διακλαδώσεις των αγγείων προς το φύλλωμα. Στην πρώτη περιοχή γίνεται η μεταφορά (transport function) του υδροδιαλύματος και στη δεύτερη περιοχή γίνεται η διανομή προς τα φύλλα (diffusive function). Στα πρώτα 3/4 του κορμού (αυτό κατά μέσο όρο, αλλά η αναλογία ύψους είναι ακόμα μεγαλύτερη στα ψηλά δέντρα), συντελείται η πρώτη λειτουργίατης μεταφροάς και στο υπόλοιπο δίκτυο η δεύτερη της διανομής. Είναι απαραίτητο λοιπόν από τη φυσιολογία του φυλλώματος να αυξηθούν τάχιστα οι διακλαδώσεις των αγγείων στην περιοχή μετάβασης μεταξύ πρώτης και δεύτερης λειτουργίας.
Στο μοντέλο Valbuena και Sopp, ο ρυθμός βασικής διακλάδωσης και ο παρεπόμενος ρυθμός διακλάδωσης των αγγείων παραμετροποιούνται καταλλήλως και έτσι προκύπτουν τα πάχη συνένωσης των αγγείων που αποτυπώνουν το όγκο του κάθε κλάδου, αλλά και του δέντρου συνολικά, καθώς προχωρούμε από τη βάση στην κορυφή. Με οποιαδήποτε παραμετροποίηση (όπως και σε προηγούμενες μελέτες) παρητηρείται αντίστροφη σχέση μεταξύ αύξησης της διατομής των αγγείων από πάνω προς κάτω και της συνένωσης αγγείων. Σε κάποια μοντέλα (όπως τα τρία πρώτα που φαίνονται στο πάνω δεξιά σχήμα), η γενική αυτή σχέση μπορεί να είναι συμβατή με την διατήρηση της εξωτερικής κυλινδρικής επιφάνειας και παρεπόμενα του αντίστοιχου όγκου του κλάδου.
Όταν όμως περνά κανείς σε μια περιοχή ταχύτατης αύξησης των διακλάδώσεων των αγγείων και των αντίστοιχων συνενώσεων, όπως συμβαίνει στη περιοχή μετάβασης από την περιοχή μεταφοράς στην περιοχή διανομής, αν ταυτόχρονα απαιτηθεί και διατήρηση της υδραυλικής αντίστασης (δηλαδή διατήρηση της ταχύτητας ροής του υδροδιαλύματος) τότε προκύπτει αναγκαστικά ότι η μείωση των διαστάσεων των αγγείων (ως προς τη διατομή αλλά και το μήκος) είναι ταχύτατη, ώστε μετά τις συνενώσεις να προκύπτει μικρότερη συνολική διατομή κλάδου και αντίστοιχα μείωση του όγκου. Δηλαδή καταρρίπτεται ο κανόνας του Leonardo, τουλάχιστον για το ανώτερο μέρος (την κόμη) του δέντρου.
Παρ΄ ότι στη μελέτη η μαθηματικοποίηση δίνει ξεκάθαρα το αναμενόμενο αποτέλεσμα (για όποιον μπορεί να ακολουθήσει την πορίεα συλλογισμών και υπολογισμών στην Πηγή 6), θα προσπαθήσω να το πω και με τη δική μου διαίσθηση του φυσικού: καθώς ολοκληρώνει το δέντρο τη μεταφορά και προετοιμάζεται για τη διανομή, στην περιοχή που αυξάνεται απότομα το πλήθος των οδών διανομής, η μείωση της διαμέτρου των αγγείων πρέπει να γίνει πολύ γρηγορότερα, ώστε να διατηρηθεί η ταχύτητα ροής. Για να "σπρώξει" τους χυμούς με επαρκή ροή πρέπει να μικρύνει πολύ πιο γρήγορα τη διατομή των τριχοειδών αγγέιων. Και έτσι προκύπτει το κάτω δεξιά σχήμα D, το οποίο δείχνει την αναγκαστική μείωση της διατομής, αν αξιώσουμε διατήρηση της ροής καθώς φτάνουμε κοντά στα φυλλώματα. Βέβαια η αληθινή επιστήμη δεν είναι μόνο διαίσθηση αλλά και υπολογισμός και η εν λόγω μελέτη φαίνεται να είναι συνεπής, ακριβής και πειστική.
Αυτή η μείωση είναι αναγκαστική, ώστε να ελαχιστοποιηθεί η ενέργεια που χρειάζεται για την μεταφορά θρεπτικών συστατικών στο φύλλωμα. Με καθαρό και σχετικά απλό υπολογισμό, προκύπτει ότι ελαχιστοποιείται επίσης και το ανθρακικό αποτύπωμα του δέντρου, καθώς απαιτείται λιγότερος άνθρακας για το δομικό ιστό του (τα τοιχώματα των αγγείων). Η φυσική επιλογή αντίστοιχα, με βάση της αρχή διατήρησης ενέργειας, έχει ευνοήσει τα φυτά που προσαρμόζουν τις παραμέτρους ανάπτυξής τους στις τοπικές συνθήκες (παροχή υδροδιαλύματος κ.λπ.).
Ο Leonardo πάντως δεν είχε κάνει και τόσο λάθος, μια και το κάτω μέρος του δέντρου δεν εμφανίζει έντονα αυτή τη στένωση, ενώ στο πάνω μέρος, εκεί όπου υφίσταται στο μικροεπίπεδο, είναι σχεδόν αδύνατο να το παρατηρήσει κανείς εμπειρικά (οι φωτογραφίες της ρωσικής μελέτης έγιναν αντικείμενο κοπιώδους επεξεργασίας πριν παραμετροποιηθούν). Για τη διδιάστατη εικόνα του κάτω μέρους του δέντρου ο Leonardo παρατηρούσε -σχεδόν- σωστά, ενώ δεν μπορούσε να εφαρμόσει τα εκλεπτυσμένα μαθηματικά και τα ισχυρά υπολογιστικά εργαλεία που μας είναι σήμερα διαθέσιμα. Προέκτεινε κατά φυσικό τρόπο την ιδέα του για τη βασιλεία της συμμετρίας στη φύση στο σύνολο του δέντρου.
Φαίνεται λοιπόν ότι δεν μπορούμε να αποφαινόμαστε θαυμαστικά και ακόμη θριαμβευτικά στο διαδίκτυο για τον περίφημο "κανόνα του Leonardo", ούτε για τις εικαστικές του επιπτώσεις ούτε για τις αεροδυναμικές του εφαρμογές. Δεν ισχύει παρά μόνο προσεγγιστικά και τοπικά (στο κάτω μέρος ενός δέντρου) και μάλιστα όχι για όλα τα δέντρα. Θα επαναλάβω πόσο εύκολα μπορεί κανείς να ακυρώσει αξιώσεις καθολικότητας παρατηρώντας τα έλατα, τα κυπαρίσσια και τις ελιές. Και όμως, λίγοι το ψάχνουν, ενώ οι περισσότεροι, εμπνεόμενοι από το όνομα Leonardo, το σερβίρουν άκοπα το διαδίκτυο, παραπέμποντας σε κάποια ρομαντική (φυσιολατρική) ανάγνωση του πράγματος.
Η φιλομάθεια όμως είναι κοπιαστικότερη άσκηση.
Πηγές:
2. Εντρυφώντας στον «Κανόνα των Δέντρων» του Λεονάρντο ντα Βίντσι - dasarxeio.com
3. The Wisdom Of Trees (Da Vinci Knew It) : NPR
5. http://pmoiras.weebly.com/uploads/4/2/4/0/42405031/Τριχοειδή_Φαινόμενα.pdf
6. Vascular optimality dictates plant morphology away from Leonardo’s rule | PNAS
7. New study disproves Leonardo da Vinci's 'rule of trees' (phys.org)
8. Leonardo da Vinci's rule for how trees branch was close, but wrong (sciencenews.org)
9. ΠΡΟΣ ΜΙΑ ΚΑΤΑΝΟΗΣΗ ΤΟΥ ΦΑΙΝΟΜΕΝΟΥ ΤΗΣ ΑΝΕΡΧΟΜΕΝΗΣ ΥΓΡΑΣΙΑΣ ΣΕ ΜΙΑ ΔΟΜΗ